Overview of Shape Variation of Epitrochoids / Epicycloids

The overview of shape variation is based on

An Epitrochoid / Epicyloid will be created by a rotation of one wheel around an other one.
In this overview all gear trains will be presented
with a single-digit transformation ratio between 1:1 and 1:9 or rather 8:9.
The derivation of the complete investigation of the shape diversity of Epitrochoids with predetermined transformation ratio can be found here.
(Look at first the result of one transformation ratio of wheels and then the derivation or vice versa)

If the cursor is over one of the images, an animation starts or something similar.

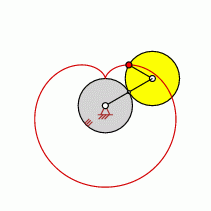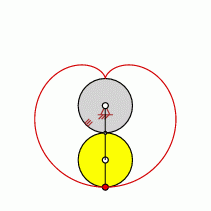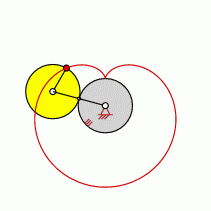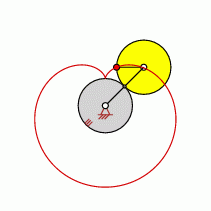
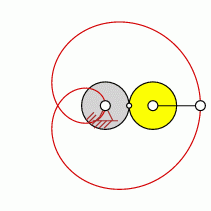
Loops=1

approximate straight-line pattern:
  0 oder 1


detailed description
transformation ratio: i=1:1
cycles U=1
intersection points:
0 oder 1

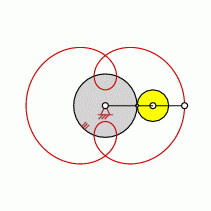
Loops=2

approximate straight-line pattern:
  0 oder 2


detailed description
transformation ratio: i=2:1
cycles U=1
intersection points:
0,2 oder 4
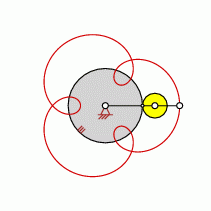
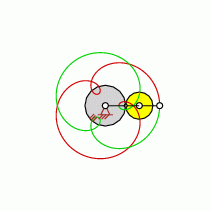
Loops=3

approximate straight-line pattern:
  0 oder 3


detailed description
transformation ratio: i=3:1
cycles U=1
intersection points:
0,3 oder 9

detailed description
transformation ratio: i=3:2
cycles U=2
intersection points:
3,6 oder 12

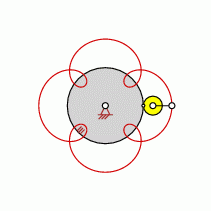
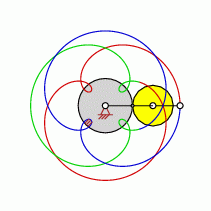
Loops=4

approximate straight-line pattern:
  0 oder 4


detailed description
transformation ratio: i=4:1
cycles U=1
intersection points:
0,4,12 oder 16

detailed description
transformation ratio: i=4:3
cycles U=3
intersection points:
8,12,202 oder 24

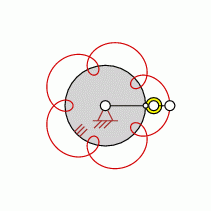
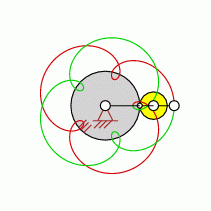
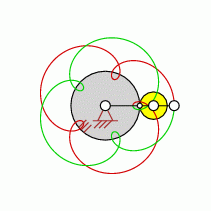
Loops=5

approximate straight-line pattern:
  0 oder 5


detailed description
transformation ratio: i=5:1
cycles U=1
intersection points:
0,5,15 oder 25

detailed description
transformation ratio: i=5:2
cycles U=2
intersection points:
5,10,20 oder 30

detailed description
transformation ratio: i=5:3
cycles U=3
intersection points:
10,15,25 oder 35

detailed description
transformation ratio: i=5:4
cycles U=4
intersection points:
15,20,30 oder 40
 

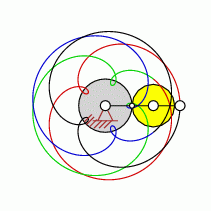
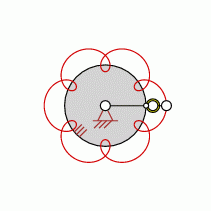
Loops=6

approximate straight-line pattern:
  0 oder 6


detailed description
transformation ratio: i=6:1
cycles U=1
intersection points:
0,6,18,30 oder 36

.
transformation ratio: i=6:5
cycles U=5
intersection points:
24,30,42,54 oder 60
 

Loops=7

approximate straight-line pattern:
  0 oder 7


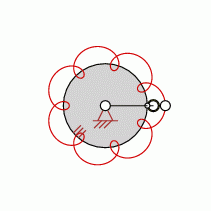
transformation ratio: i=7:1
cycles U=1
intersection points:
0,7,21,35 oder 49

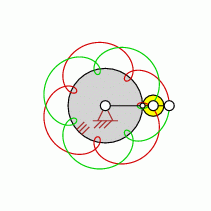
transformation ratio: i=7:2
cycles U=2
intersection points:
7,14,28,42 oder 56

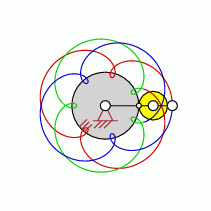
transformation ratio: i=7:3
cycles U=3
intersection points:
14,21,35,49 oder 63

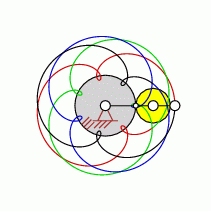
transformation ratio: i=7:4
cycles U=4
intersection points:
21,28,42,56 oder 70

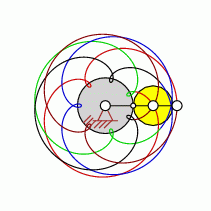
transformation ratio: i=7:5
cycles U=5
intersection points:
28,35,49,63 oder 77

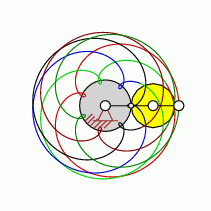
transformation ratio: i=7:6
cycles U=6
intersection points:
35,42,56,70 oder 84
 

Loops=8

approximate straight-line pattern:
  0 oder 8


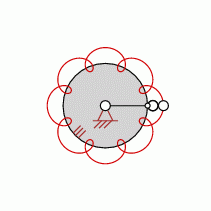
transformation ratio: i=8:1
cycles U=1
intersection points:
0,8,24,40,56 oder 64

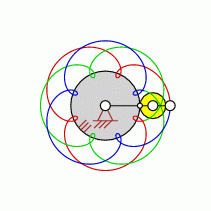
transformation ratio: i=8:3
cycles U=3
intersection points:
16,24,40,56,72 oder 80

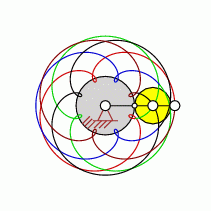
transformation ratio: i=8:5
cycles U=5
intersection points:
32,40,56,72,88 oder 96

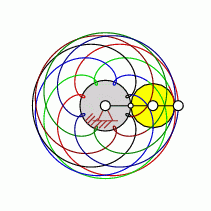
transformation ratio: i=8:7
cycles U=7
intersection points:
48,56,72,104 oder 102
 

Loops=9

approximate straight-line pattern:
  0 oder 9


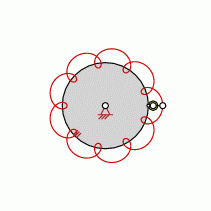
transformation ratio: i=9:1
cycles U=1
intersection points:
0,9,18,36,54,72 oder 90

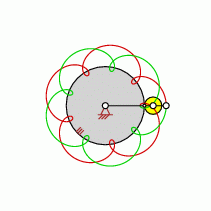
transformation ratio: i=9:2
cycles U=2
intersection points:
9,27,45,63 oder 81

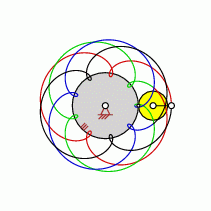
transformation ratio: i=9:4
cycles U=4
intersection points:
27,36,54,72,90 oder 108

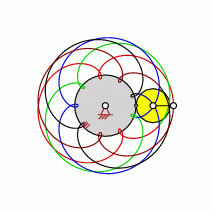
transformation ratio: i=9:5
cycles U=5
intersection points:
36,45,63,81,99 oder 117

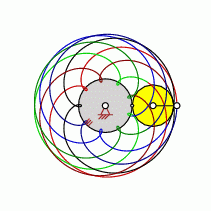
transformation ratio: i=9:7
cycles U=7
intersection points:
54,63,81,99,117 oder 135

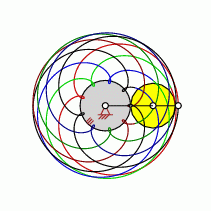
transformation ratio: i=9:8
cycles U=8
intersection points:
63,72,90,108,126 oder 144

Recapitulation of the links of this page:

 

© Volker Jaekel, October 25th 2015

eMail: V.Jaekel@t-online.de