Epitrochoid / Epicycloid: Shape Variation for a transmission ratio of 1:1 including the special shape of cardioid

The overview of shape variation is based on

• the number of loops and cusps (sharp corners)
• the number of approximate straight-line pattern
• the number of self-tangential points
• the number of self-intersection points
• the number of alterations of the center of curvature from one side to the other side of the Epitrochoid
  (change from left to right turns)

The circles are known, which borders the rings. They are called

• the BALL Points are forming a circle. Epritochoids created by BALL Points pass through an approximate straight-line pattern
• the Moving Centrode is identical with the tread of wheel. Its points pass through Epritochoids with cusps.
• the Transition Curve (Uebergangskurve so called by by R. Mueller) with points passing through self-tangential points of Epitrochoids. The Number of Transition Curves varies between 0, 1 and a number greater than 1.
  (In this case the number is equal 0. With other words: In this case no Transition Curve exists and as result no Epitrochoide will be created with self-tangential points.)

The epitrochoid is created by a point, and if this point moves from the inner edge of the ring on the ring-shaped surface, then the shape of the epitrochoid changes. The same applies when switching from the ring-shaped surface to the outer edge. If the generating point varies its location within the ring-shaped surface, then the epitrochoid itself varies, but there is no qualitative modification of the epitrochoid (the verbal description does not change).

The following table describes alternately the shape of an epitrochoid

1. if the generating point is part of the inner edge of a ring
2. if the generating point is part of the ring-shaped surface

• If the point is located on the outer edge of a ring, it is coinstantaneous the inner edge of the next larger ring. Thus the description 2 follows the description 1 on the ring next size up

In the middle of all rings is a disc whose center point is the inner edge of a "disc-shaped ring." The table begins with this center point.

---

	Number of loops 1 transformation ratio i=1:1 Number of cycles 1	Remarks about the point, which creates the epitrochoid Remark about the shape of the epitochoid
The point (which created the epitrochoid) is on the edge of a ring approximate straight-line patterns 0 cusps 0 self-intersection points 0 self-tangential points 0 number of alterations of the center of curvature 0		Point is identical with the center of the wheel The epitrochoid is a circle
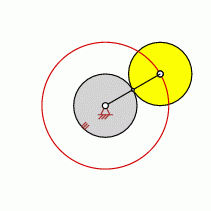
The point (which created the epitrochoid) is on the ring-shaped surface approximate straight-line patterns 0 cusps 0 self-intersection points 0 self-tangential points 0 number of alterations of the center of curvature 0		Point resides on the ring-shaped surface between the center of the wheel and the BALL Circle (BALL Curve) The center of curvature does not alternate to the other site of the curve.
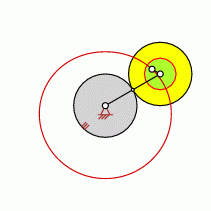
The point (which created the epitrochoid) resides on the edge of a ring approximate straight-line patterns 1 cusps 0 self-intersection points 0 self-tangential points 0 number of alterations of the center of curvature 0		The point is a part of the BALL Circle (BALL Curve) The BALL Circle resides always between the pivot and the outer edge of the moving wheel The radius of the BALL Circle is 0.5 for this transmission ratio (multiplied by the radius of the moving wheel)
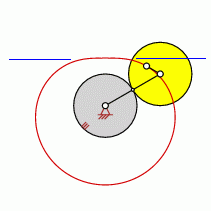
The point (which created the epitrochoid) is on the ring-shaped surface approximate straight-line patterns 0 cusps 0 self-intersection points 0 self-tangential points 0 number of alterations of the center of curvature 2		Point resides between the BALL Circle (BALL Curve) and the Moving Centrode
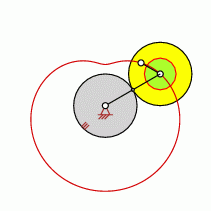
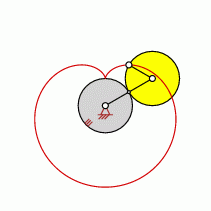
The point (which created the epitrochoid) is on the edge of a ring approximate straight-line patterns 0 cusps 1 self-intersection points 0 self-tangential points 0 number of alterations of the center of curvature 0		Point is part of the Moving Centrode The Moving Centrode is identical with the tread of the moving wheel. The radius of the circular Moving Centrode is 1.0 (multiplied by the radius of the moving wheel) In this case is is the special special type cardioid
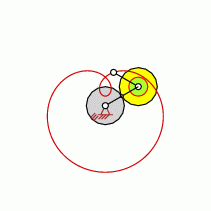
The point (which created the epitrochoid) is on the ring-shaped surface approximate straight-line patterns 0 cusps 0 self-intersection points 1 self-tangential points 0 number of alterations of the center of curvature 0		Point is outside of the Moving Centrode (outside of the tread of the wheel) No Transition Curve exists for this transmission ratio.

Recapitulation of the links of this page:

• The derivation of the complete investigation of the shape diversity of Epitrochoids
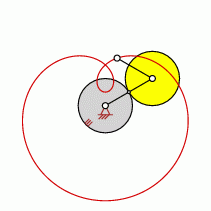• Overview of Shape Variation of Epitrochoids
• Animation of trochoids

© Volker Jaekel, January third 2024

eMail: V.Jaekel@t-online.de