|
| Anzahl Schleifen |
2
|
| Übersetzung |
i=2:1
|
| Anzahl Umläufe |
1
|
|
Bemerkungen zu dem die Hypotrochoide erzeugenden Punkt
- Bermerkungen zur Form der Hypotrochoide
|
|
Erzeugende Punkt liegt im Mittelpunkt eines Rings
|
|
| Genäherte Geradführungen |
0 |
| Spitzen |
0 |
| Selbstschnittpunkte |
0 |
| Selbstberührungspunkte |
0 |
Seitenwechsel des
Krümmungsmittelpunktes
|
0 |
|
|
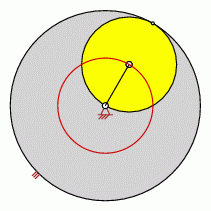
Punkt ist identisch mit Mittelpunkt des Rades
- Hypotrochoide ist ein Kreis
|
|
Erzeugende Punkt liegt auf Fläche eines Rings
|
|
| Genäherte Geradführungen |
0 |
| Spitzen |
0 |
| Selbstschnittpunkte |
0 |
| Selbstberührungspunkte |
0 |
Seitenwechsel des
Krümmungsmittelpunktes
|
0 |
|
|
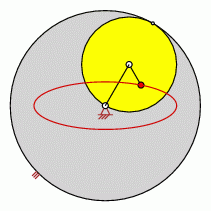
Punkt liegt zwischen Mittelpunkt des Rades und BALLschem Kreis (BALLscher Kurve)
- Der Krümmungsmittelpunkt der Bahn wechselt nicht die Seite.
|
|
Erzeugende Punkt liegt auf Rand eines Rings
|
|
| Genäherte Geradführungen |
2
|
| Spitzen |
2
|
| Selbstschnittpunkte |
0 |
| Selbstberührungspunkte |
0 |
Seitenwechsel des
Krümmungsmittelpunktes
|
0 |
|
|
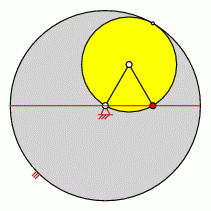
Punkt liegt auf dem BALLschen Kreis (der BALLschen Kurve)
- Der BALLscher Kreis befindet sich zwischen Mittelpunkt und Rand des umlaufenden Rades
- In diesem Sonderfall ist der BALLsche Kreis mit dem Rand des umlaufenden Rades identisch
- Das bedeutet gleichzeitig, dass der BALLsche Kreis mit der Gangpolkurve identisch ist
- Punkte auf der Gangpolkurve erzeugen Spitzen
- In diesem Fall handelt es sich nicht nur um genäherte Geradführungen, es sind echte Geraden.
-
Der Radius des Ballschen Kreises ist bei dieser Übersetzung
1
(multipliziert mit dem Radius des umlaufenden Rades)
|
|
Erzeugende Punkt liegt auf Fläche eines Rings
|
|
| Genäherte Geradführungen |
0 |
| Spitzen |
0 |
| Selbstschnittpunkte |
0
|
| Selbstberührungspunkte |
0 |
Seitenwechsel des
Krümmungsmittelpunktes
|
0 |
|

|
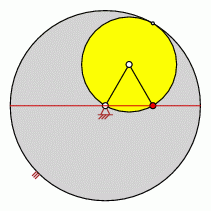
Punkt liegt außerhalb der Gangpolkurve (außerhalb des umlaufenden Rades)
- Es treten keine Übergangskurven bei diesem Übersetzungsverhältnis auf.
|






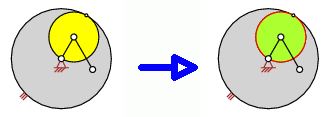 Die Kreise, die die Ränder der Ringe bilden, sind bekannt. Es handelt sich um
Die Kreise, die die Ränder der Ringe bilden, sind bekannt. Es handelt sich um
 Ein solcher Sonderfall liegt hier
nicht
vor.
Ein solcher Sonderfall liegt hier
nicht
vor.